Elemi részecskék és kölcsönhatásaik
Tartalomjegyzék
A részecskefizika egységrendszere
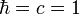 <toggledisplay>
Compton-hullámhossz:[KÉNE MAGYARÁZAT!!!]
<toggledisplay>
Compton-hullámhossz:[KÉNE MAGYARÁZAT!!!]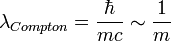
Átlagos élettartam: 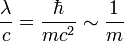
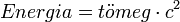 ,
, 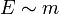
Részecskék tömege: eV, MeV, GeV stb. (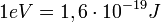 ).
). 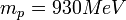 ,
, 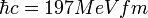 </toggledisplay>
</toggledisplay>
Részecskeosztályozás és kölcsönhatások
Elemi részecske:[1] Az elérhető legnagyobb energiákon sincs belső szerkezet. [2]
Az elemi részecskék jellemzői
- m (nyugalmi tömeg)[3]
- s (spin)
- töltések [RÉSZLETEZENDŐ!!!]
- mágneses momentum
XX. század elején az elemi részecskék az elektron, proton, foton(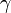 ), neutrínó (
), neutrínó (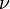 ). Aztán felfedezték a
). Aztán felfedezték a 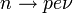 reakciót, ami a gyenge kölcsönhatás egyik jó példája.
reakciót, ami a gyenge kölcsönhatás egyik jó példája.
Mai képünk az anyagról
| osztály | jelölés | spin | töltés |
| kvarkok | q |  spin spin |
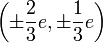 "bezárás" [4] "bezárás" [4]
|
| leptonok | l |  spin spin |
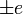 , vagy 0 - neutrínók , vagy 0 - neutrínók
|
Kölcsönhatások közvetítése
| név | közvetítő bozonok (egész spin) | közvetítő részecske tömege | hatótávolsága |
| gravitációs | 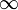
| ||
| elektromágneses | foton (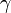 ) ) |
0 | 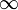
|
| gyenge | 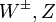 -bozonok -bozonok |
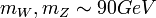 |
rövid (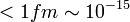 ) )
|
| erős | gluon (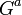 ) ) |
0 ("bezárás") | rövid (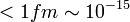 ) )
|
A részecskékre igaz a Pauli-elv (hu en), azaz:
- Azonos fermionok aszimmetrikus,
- azonos bozonok szimmetrikus hullámfüggvényt valósítanak meg.
A hullámfüggvény szorzatalkú, egy térbeli rész és egy spint tartalmazó rész szorzataként írható fel: 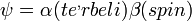 .
.
A térbeli rész a relatív koordinátáktól függ: 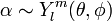 [5]
[5]
Felcserélésnél: 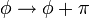 és
és 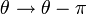
Minthogy fermionok esetén a hullámfüggvénynek aszimmetrikusnak, bozonok esetén pedig szimmetrikusnak kell lennie, ezen típusú részecskék esetén 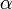 és
és 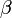 értékére a következő lehetőségek adódnak:
értékére a következő lehetőségek adódnak:
| típus | 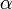 |
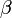
|
| fermionok | aszimmetrikus | szimmetrikus |
| szimmetrikus | aszimmetrikus | |
| bozonok | szimmmetrikus | szimmetrikus |
| aszimmetrikus | aszimmetrikus |
Példa
<toggledisplay>
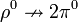 , mivel a
, mivel a 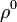 1-es spinű, a
1-es spinű, a 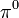 pedig 0-s spinű, és mindkettő bozon.
pedig 0-s spinű, és mindkettő bozon. 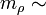 770 MeV,
770 MeV, 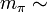 130 MeV.
130 MeV.
Mivel az impulzusmomentum a jelen folyamat esetén megmarad, és a kiindulásnál 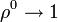 , ezért
, ezért 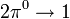 -nek kell lennie (és mivel
-nek kell lennie (és mivel 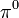 -nak nincs, csak a pályaimpulzusmomentumból lehet, viszont a Pauli-elv nem engedi, hogy a
-nak nincs, csak a pályaimpulzusmomentumból lehet, viszont a Pauli-elv nem engedi, hogy a 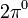 pályaimpulzusmomentuma 1 legyen).
pályaimpulzusmomentuma 1 legyen).
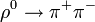
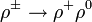
Mivel a fentiek a jobb oldalon nem azonos részecskék. </toggledisplay>
Antirészecskék: a tömeg és a spin ugyanaz, a töltése pedig -1-szeres, például: 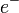 (elektron) -
(elektron) - 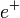 (pozitron),
(pozitron), 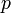 (proton) -
(proton) - 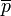 (antiproton).
(antiproton).
Kvarkok
Barionszámuk 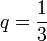 , az antikvarkoké
, az antikvarkoké 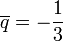 . A kvarkok hat "ízben" (flavour) vannak jelen a természetben.
. A kvarkok hat "ízben" (flavour) vannak jelen a természetben.
- ↑ Ritkán, de használják a szubnukleáris részecske elnevezést is. Szubnukleáris részecske: ami az atomokban nem található meg.
- ↑ Ez természetesen időfüggő. Száz éve még eleminek gondolt részecskékről kiderült, hogy nem azok, nagyobb energiájú gyorsítókban végzett kísérletek során.
- ↑ A tanár úr kiemelte, hogy jelen előadásban a mozgási tömeget, mint fogalmat nem használja, minden további tömeg nyugalmi tömegnek értendő.
- ↑ Szabad kvarkot még nem figyeltek meg és a jelenlegi elméletek szerint nem is lehet.
- ↑ Itt felírtunk valamit arról, hogy
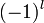 , de az mire is vonatkozott pontosan? Aki tudja, javítsa ki legyen szíves.
, de az mire is vonatkozott pontosan? Aki tudja, javítsa ki legyen szíves.