„Adatelemzés: ARCH, GARCH folyamatok” változatai közötti eltérés
(Új oldal, tartalma: „==ARCH, GARCH modellek== *ARCH: autoregressive conditionally heteroscedastic; időben változó volatilitás (szórás, variancia) – mivel gazdasági idősorokra szokt…”) |
|||
| 7. sor: | 7. sor: | ||
A legegyszerűbb ARCH modell az ARCH(1) modell: | A legegyszerűbb ARCH modell az ARCH(1) modell: | ||
| − | <math>y_t = \sigma_t \epsilon_t </math> | + | <math>y_t = \sigma_t \epsilon_t </math> (1) |
| − | <math>\sigma_t^2 = \alpha_0 + \alpha_1 y_{t-1}^2</math> | + | <math>\sigma_t^2 = \alpha_0 + \alpha_1 y_{t-1}^2</math> (2) |
| − | <math>y_t</math> az idősor értéke t-ben, <math>\sigma_t<math> a szórás t-ben, <math>\epsilon_t<math> standard normál eloszlásból származó zaj, <math>\alpha_1<math> legyen nemnegatív. | + | <math>y_t</math> az idősor értéke t-ben, <math>\sigma_t</math> a szórás t-ben, <math>\epsilon_t</math> standard normál eloszlásból származó zaj, <math>\alpha_1</math> legyen nemnegatív. |
| − | A <math>\sigma_t^2<math>-re AR modellt írtunk fel. | + | A <math>\sigma_t^2</math>-re AR modellt írtunk fel. |
Miért is kell feltételes eloszlásról beszélni (ar conditionally h)? Ha az idősor stacionárius lenne, vagyis az összes elem azonos eloszlásból származna, egy későbbi érték eloszlása megegyezne a hosszú távú, feltétel nélküli eloszlással. A nem stacionárius idősorokra időben változhat a szórás, ezt ha figyelembe vesszük, akkor kapjuk a feltételes eloszlást. | Miért is kell feltételes eloszlásról beszélni (ar conditionally h)? Ha az idősor stacionárius lenne, vagyis az összes elem azonos eloszlásból származna, egy későbbi érték eloszlása megegyezne a hosszú távú, feltétel nélküli eloszlással. A nem stacionárius idősorokra időben változhat a szórás, ezt ha figyelembe vesszük, akkor kapjuk a feltételes eloszlást. | ||
| − | <math>y_t<math> feltételes eloszlása gaussi: <math>y_t | + | <math>y_t</math> feltételes eloszlása gaussi: <math>y_t | y_{t-1} \sim N(0, \alpha_0 + \alpha_1 y_{t-1}^2)</math> |
| + | |||
Az (1) és (2) egyenleteket 0-ra rendezve, egyenlővé téve, majd átrendezve a következőt kapjuk: | Az (1) és (2) egyenleteket 0-ra rendezve, egyenlővé téve, majd átrendezve a következőt kapjuk: | ||
| − | |||
| − | |||
| − | Állítás: | + | <math>y_t^2=\alpha_0+\alpha_1 y_{t-1}^2+\sigma_t^2 (\epsilon_t^2-1)</math> |
| − | Biz.: legyen | + | |
| + | Ez egy nem-gaussi AR(1) modell az <math>y_t^2</math>-re felírva. | ||
| + | |||
| + | ==Állítás: <math>y_t</math> átlaga 0== | ||
| + | |||
| + | Biz.: legyen <math>Y_s = \{y_s, y_s-1, \ldots, y_0}<\math>, ekkor, mivel yt csak yt-1-től függ, az pedig egy nulla átlagú gauss: | ||
E(y_t )=E(y_t│Y_t )=E(y_t│y_(t-1) )=0 | E(y_t )=E(y_t│Y_t )=E(y_t│y_(t-1) )=0 | ||
Áll.: yt korrelálatlan | Áll.: yt korrelálatlan | ||
| 36. sor: | 40. sor: | ||
Ha a nevező pozitív, akkor ez mindig nagyobb lesz 3-nál (3 a normál eo. kurtózisa), vagyis ez egy vastag farkú (fat tail) eloszlás lesz. | Ha a nevező pozitív, akkor ez mindig nagyobb lesz 3-nál (3 a normál eo. kurtózisa), vagyis ez egy vastag farkú (fat tail) eloszlás lesz. | ||
| − | ARCH(1) kiterjesztése ARCH(m)-re | + | ==ARCH(1) kiterjesztése ARCH(m)-re== |
| − | y_t= | + | <math>y_t = \sigma_t \epsilon_t</math> |
| − | + | ||
| − | + | <math>\sigma_t^2 = \alpha_0 + \alpha_1 y_{t-1}^2+\alpha_2 y_{t-2}^2 + \ldots + \alpha_m y_{t-m}^2</math> | |
| + | |||
| + | <math>y_t</math> feltételes eloszlása ismét gaussi: <math>y_t | y_{t-1} \sim N \left(0, \alpha_0 + \alpha_1 y_{t-1}^2 + \alpha_2 y_{t-2}^2 + \ldots + \alpha_m y_{t-m}^2\right)</math> | ||
| − | A legáltalánosabb GARCH(m,r) modell | + | ==A legáltalánosabb GARCH(m,r) modell== |
Ha megvan a paraméterbecslés (pl: maximum likelihood-dal), akkor jóslást tehetünk a volatilitásra (csak 1 lépésre előre!): | Ha megvan a paraméterbecslés (pl: maximum likelihood-dal), akkor jóslást tehetünk a volatilitásra (csak 1 lépésre előre!): | ||
| − | |||
Paraméterbecslés ARCH(1) modellre: maximum likelihood | Paraméterbecslés ARCH(1) modellre: maximum likelihood | ||
| − | az f() függvény az | + | az f() függvény az <math>y_t</math> feltételes eloszlása: <math>N(0, \alpha_0 + \alpha_1 y_{t-1}^2)</math> |
| − | A –ln(L) minimuma fogja megadni az | + | |
| + | A –ln(L) minimuma fogja megadni az <math>\alpha_0</math> és <math>\alpha_1</math> paramétereket. | ||
A lap 2011. június 7., 16:12-kori változata
ARCH, GARCH modellek
- ARCH: autoregressive conditionally heteroscedastic; időben változó volatilitás (szórás, variancia) – mivel gazdasági idősorokra szokták alkalmazni, a volatilitás a használt kifejezés
- GARCH: generalized ARCH
A legegyszerűbb ARCH modell az ARCH(1) modell:
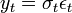 (1)
(1)
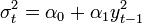 (2)
(2)
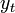 az idősor értéke t-ben,
az idősor értéke t-ben, 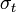 a szórás t-ben,
a szórás t-ben, 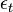 standard normál eloszlásból származó zaj,
standard normál eloszlásból származó zaj, 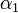 legyen nemnegatív.
legyen nemnegatív.
A 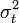 -re AR modellt írtunk fel.
-re AR modellt írtunk fel.
Miért is kell feltételes eloszlásról beszélni (ar conditionally h)? Ha az idősor stacionárius lenne, vagyis az összes elem azonos eloszlásból származna, egy későbbi érték eloszlása megegyezne a hosszú távú, feltétel nélküli eloszlással. A nem stacionárius idősorokra időben változhat a szórás, ezt ha figyelembe vesszük, akkor kapjuk a feltételes eloszlást.
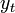 feltételes eloszlása gaussi:
feltételes eloszlása gaussi: 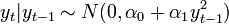
Az (1) és (2) egyenleteket 0-ra rendezve, egyenlővé téve, majd átrendezve a következőt kapjuk:
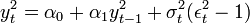
Ez egy nem-gaussi AR(1) modell az 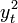 -re felírva.
-re felírva.
Állítás: 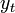 átlaga 0
átlaga 0
Biz.: legyen Értelmezés sikertelen (Hiányzó <code>texvc</code> végrehajtható fájl; a beállítást lásd a math/README fájlban.): Y_s = \{y_s, y_s-1, \ldots, y_0}<\math>, ekkor, mivel yt csak yt-1-től függ, az pedig egy nulla átlagú gauss: E(y_t )=E(y_t│Y_t )=E(y_t│y_(t-1) )=0 Áll.: yt korrelálatlan Biz.: cov(y_(t+h),y_t )=E(y_t y_(t+h) )=E(y_t y_(t+h)│Y_(t+h-1) )=E(y_t E(y_(t+h)│Y_(t+h-1) ))=0, ha h≠0 Kiszámolhatjuk yt2 és yt4 átlagát (az első könnyű, csak az AR modell képletét alkalmazzuk): E(y_t^2 )=α_0/(1-α_1 ) E(y_t^4 )=(3α_0^2)/(1-α_1 )^2 (1-α_1^2)/(1-3α_1^2 ) Ez a két érték a kurtózis kiszámolásához kellett: Ha a nevező pozitív, akkor ez mindig nagyobb lesz 3-nál (3 a normál eo. kurtózisa), vagyis ez egy vastag farkú (fat tail) eloszlás lesz. ==ARCH(1) kiterjesztése ARCH(m)-re== <math>y_t = \sigma_t \epsilon_t
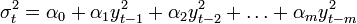
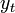 feltételes eloszlása ismét gaussi:
feltételes eloszlása ismét gaussi: 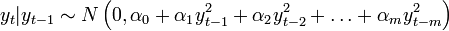
A legáltalánosabb GARCH(m,r) modell
Ha megvan a paraméterbecslés (pl: maximum likelihood-dal), akkor jóslást tehetünk a volatilitásra (csak 1 lépésre előre!):
Paraméterbecslés ARCH(1) modellre: maximum likelihood
az f() függvény az 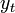 feltételes eloszlása:
feltételes eloszlása: 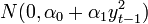
A –ln(L) minimuma fogja megadni az 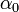 és
és 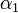 paramétereket.
paramétereket.