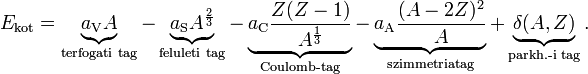„Félempirikus kötési formula” változatai közötti eltérés
(Tagmagyarázat) |
(Hibajavítás) |
||
| 1. sor: | 1. sor: | ||
| − | A kötési energia | + | A kötési energia: |
| − | <math> | + | <math>E_{\text{kot}} = \underbrace{a_{\text{V}}A}_{\text{terfogati tag}}-\underbrace{a_{\text{S}}A^{\frac{2}{3}}}_{\text{feluleti tag}}-\underbrace{a_{\text{C}}\frac{Z(Z-1)}{A^{\frac{1}{3}}}}_{\text{Coulomb-tag}}-\underbrace{a_{\text{A}}\frac{(A-2Z)^2}{A}}_{\text{szimmetriatag}} + \underbrace{\delta(A,Z)}_{\text{parkh.-i tag}}.</math> |
A lap jelenlegi, 2011. június 26., 23:34-kori változata
A kötési energia: