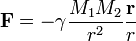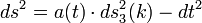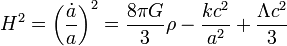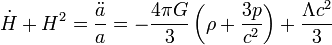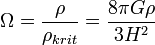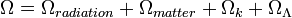„Az asztrofizika alapjai” változatai közötti eltérés
(→A HR diagram és a csillagfejlődés szemléletes képe, kompakt objektumok: fehér törpék, neutroncsillagok, fekete lyukak, csillagok energiatermelése) |
Rudi (vitalap | szerkesztései) (→Megfigyelés alapjai: luminozitás, magnitúdó, vöröseltolódás) |
||
| (23 közbenső módosítás, amit 3 másik szerkesztő végzett, nincs mutatva) | |||
| 2. sor: | 2. sor: | ||
A gravitáció négy alapvető kölcsönhatás egyike az univerzumban, és az egyetlen amely a nagyskálás szerkezetet meghatározza. A legkorábbi kvantitatív megfogalamzása Newton-hoz köthető: | A gravitáció négy alapvető kölcsönhatás egyike az univerzumban, és az egyetlen amely a nagyskálás szerkezetet meghatározza. A legkorábbi kvantitatív megfogalamzása Newton-hoz köthető: | ||
| − | :<math>F = \gamma\frac{M_1 M_2}{r^2}</math> | + | :<math>\mathbf{F} = -\gamma\frac{M_1 M_2}{r^2}\frac{\mathbf{r}}{r}</math> |
| − | azaz az elektrosztatikus Coulomb-törvényhez hasonló alakú, reciproknégyzetes lecsengésű erő, amely azonban csak vonzó formában ismert. A Newton-i erőtörvény igen jó leírását adta a gravitációs jelenségeknek | + | azaz az elektrosztatikus Coulomb-törvényhez hasonló alakú, reciproknégyzetes lecsengésű erő, amely azonban csak vonzó formában ismert. A Newton-i erőtörvény igen jó leírását adta a gravitációs jelenségeknek, a kevés hiányosságot Einstein általános relativitáselmelete pótolta. Ez utóbbi határeseteként tartalmazza a Newton-i erőtörvényt. |
== Az ősrobbanás elmélet alapvető feltevései == | == Az ősrobbanás elmélet alapvető feltevései == | ||
A Big Bang modell a kozmológia Standard modellje. Elsősorban megfigyelésekre és az általános relativitáselméletre épül. | A Big Bang modell a kozmológia Standard modellje. Elsősorban megfigyelésekre és az általános relativitáselméletre épül. | ||
| − | * Az univerzum megfigyelések szerint nagy skálán ( | + | * Az univerzum megfigyelések szerint nagy skálán (100 MPc felett) homogén (az anyag eloszlása egyenletes), erre alapul a kozmológiai elv, vagyis az a feltételezés, hogy univerzum homogén és izotrop. |
| − | * | + | * Megfigyelések szerint az univerzum tágul (a Hubble-törvénynek megfelelően), ha ezt a folyamatot időben megfordítjuk, akkor eljutunk az ősrobbanás alap gondolatához. |
| − | * | + | Az ősrobbanás modelljének legfontosabb bizonyítékai: |
| + | * [[Hubble-törvény]] | ||
| + | * Könnyű elemek előfordulási gyakorisága (75% H és 25% He) | ||
| + | * [[Kozmikus háttérsugárzás]] | ||
== Friedmann-egyenletek szemléletes értelme == | == Friedmann-egyenletek szemléletes értelme == | ||
| − | Az univerzum tágulásának tárgyalásakor elengedhetetlen az általános relativitás elmélet kereteiben történő tárgyalás. Tömören összefoglalva a tér-idő távolságokat magábanfoglaló ívelemnégyzet (lásd [[A_relativitás_elmélet_alapjai#Relativisztikus_fizika | itt]]) függ a helytől, és ez a függés kapcsolatban van a tömegekkel. A helyfüggést leíró görbületi tenzor, és az anyag állapotegyenletét magábanfoglaló feszültségtenzor között az Einstein-egyenletek teremtenek kapcsolatot. Ha a tágulást egy skálafaktorral (a) jellemezzük az ívelemben: | + | Az univerzum tágulásának tárgyalásakor elengedhetetlen az általános relativitás elmélet kereteiben történő tárgyalás. Tömören összefoglalva a tér-idő távolságokat magábanfoglaló ívelemnégyzet (lásd [[A_relativitás_elmélet_alapjai#Relativisztikus_fizika | itt]]) függ a helytől, és ez a függés kapcsolatban van a tömegekkel. A helyfüggést leíró görbületi tenzor, és az anyag állapotegyenletét magábanfoglaló feszültségtenzor között az Einstein-egyenletek teremtenek kapcsolatot. Ha az univerzum homogén és izotróp, akkor a Robertson-Walker metrika használható, ahol a tágulást egy skálafaktorral (a) jellemezzük az ívelemben: |
| − | :<math>ds^2 = a(t)\cdot ds_3(k) - dt^2 </math> | + | :<math>ds^2 = a(t)\cdot ds_3^2(k) - dt^2 </math> |
| − | itt <math>ds_3(k)</math> a háromdimenziós | + | itt <math>ds_3^2(k)</math> a háromdimenziós ívelemnégyzet függ a térkoordinátáktól, ami különböző geometriájú unierzumoknak felel meg, ezeket ''k'' paraméterezi. A fenti ívelemmel az univerzum tágulását leíró Friedmann-egyenletek homogén, izotrop közelítésben: |
:<math>H^2 = \left(\frac{\dot{a}}{a}\right)^2 = \frac{8 \pi G}{3} \rho - \frac{kc^2}{a^2} + \frac{\Lambda c^2}{3}</math> | :<math>H^2 = \left(\frac{\dot{a}}{a}\right)^2 = \frac{8 \pi G}{3} \rho - \frac{kc^2}{a^2} + \frac{\Lambda c^2}{3}</math> | ||
| 24. sor: | 27. sor: | ||
Ezek a kozmológia alapegyenletei. | Ezek a kozmológia alapegyenletei. | ||
| − | ''H'' a Hubble- | + | ''H'' a Hubble-paraméter, amely az univerzum tágulását jellemzi és aminek a mai értéke a Hubble-konstans, ''G'' a gravitációs konstans, <math>\Lambda</math> a kozmológiai konstans, ''c'' a fénysebesség, ''k'' az univerzum görbületét jellemző mennyiség (sík, gömb, vagy hiperbolikus felület). A kozmológiai állandó olyan, hogy pozitív energiasűrűséghez negatív nyomást rendel. Ezzel magyarázzák ma a gyorsuló tágulást, és ezt tartalmazzák a Friedmann egyeletek legjobboldalibb tagjai. Ezért felelős az úgynevezett sötét energia, amiről ma még nem tudjuk, hogy mi is valójában. |
| − | + | <math>k</math> a téridő általános geometriáját adja meg: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
*A <math>k=+1</math> megfelel a pozítív görbületű, zárt térnek, mely határtalan, de véges. Az ilyen geometriájú táguló Univerzum két dimenzióban felfúvódó léggömbbel szemléltethető. Az ilyen térben a háromszög szögeinek összege több, mint 180 fok. | *A <math>k=+1</math> megfelel a pozítív görbületű, zárt térnek, mely határtalan, de véges. Az ilyen geometriájú táguló Univerzum két dimenzióban felfúvódó léggömbbel szemléltethető. Az ilyen térben a háromszög szögeinek összege több, mint 180 fok. | ||
| 39. sor: | 36. sor: | ||
*<math>k=0</math>-nál sík, euklidészi térről van szó. | *<math>k=0</math>-nál sík, euklidészi térről van szó. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Az egyenletet átalakítva relativisztikus és nem relativisztikus esetekben a következő arányosságokat kaphatjuk: | Az egyenletet átalakítva relativisztikus és nem relativisztikus esetekben a következő arányosságokat kaphatjuk: | ||
| 50. sor: | 41. sor: | ||
a, Relativisztikus esetben (sugárzás dominálta univerzum) felhasználva, hogy a nyomás és a sűrűség között a <math>p = 3\rho</math> összefüggés áll fenn: | a, Relativisztikus esetben (sugárzás dominálta univerzum) felhasználva, hogy a nyomás és a sűrűség között a <math>p = 3\rho</math> összefüggés áll fenn: | ||
| − | <math>\rho \propto | + | <math>\rho \propto a^{-4}</math> és <math>a \propto t^{1/2}</math> |
| − | + | b, Nem relativisztikus esetben (anyag dominálta univerzum) esetén pedig <math>p = 0</math> összefüggés teljesülése mellett: | |
| − | <math> | + | <math>\rho \propto a^{-3}</math> és <math>a \propto t^{2/3}</math> |
| − | + | Definiálhatjuk az <math>\Omega</math> sűrűség paramétert. Ez szemléletesen az univerzum időfejlődését paraméterezi, ha 1-nél kisebb az univerzum örökké tágul, ha 1-el egyenlő akkor a végtelenségig lassul a tágulás, ha nagyobb, akkor egy időután újra összeroppan. | |
| − | <math>\rho \ | + | :<math>\Omega = \frac{\rho}{\rho_{krit}}=\frac{8 \pi G \rho}{3H^2}</math> |
| − | + | ahol <math>\rho_{krit}</math> értékét úgy kaphatjuk meg, hogy az első Friedmann egyenletben vesszük a <math>\Lambda=0</math> és <math>k=0</math> esetet. Ma úgy gondoljuk, hogy <math>\rho=\rho_{krit}</math>, tehát <math>\Omega=1</math>, amit fel lehet írni az univerzum különböző összetevőinek az összegeként: | |
| − | <math> | + | :<math>\Omega = \Omega_{radiation}+\Omega_{matter}+\Omega_k+\Omega_\Lambda</math> |
| + | ahol ma <math>\Omega_k\simeq{0}</math>, <math>\Omega_{radiation}<<1</math>, <math>\Omega_{matter}=0,3</math> és <math>\Omega_\Lambda=0,7</math>. Itt az <math>\Omega_{matter}</math>-be tartozik mind a látható, mind a sötét anyag (<math>\Omega_{darkmatter}=0,25</math>). | ||
| − | + | == Galaxisok kialakulása, morfológiája, Hubble törvény == | |
| + | A galaxisok főleg hidrogénből és héliumból keletkeztek a saját gravitációjuk hatására. Két elmélet létezik: | ||
| − | : | + | * Felülről lefelé elmélet: A csillagközi H-ből és He-ból nagy a mai galaxisok méretével összemérhető felhők alakultak ki a saját gravitációjuk miatt, majd ezekben születtek meg a csillagok, amikortól már galaxisnak tekinthetők ezek a képződmények. |
| − | + | * Alulról felfelé elmélet: A csillagközi H és He kis méretű felhőkké állt össze, ezekben születtek az első csillagok. Majd ezek a kis méretű galaxisok ütköztek, és így álltak össze nagy galaxisokká. | |
A galaxisok osztályozását a Hubble diagram szemlélteti: | A galaxisok osztályozását a Hubble diagram szemlélteti: | ||
| 78. sor: | 71. sor: | ||
Hubble-törvény: <math>v=Hr</math> ahol H a Hubble-állandó (71 km/s/Mpc). A Hubble-állandó pontos mérése nagyon fontos, mert a Hubble-törvényben szerelő sebességet a vörös eltolódás alapján meg tudják mérni, és így ez alapján lehet egy galaxis távolságát meghatározni. Sokáig viszont nem tudták pontosan megmérni a Hubble-állandót, csak nagyságrendileg tudták meghatározni, ezért azt mondták, hogy <math>H=100h</math> km/s/Mpc, és <math>h</math>-t meghagyták a képletekben paraméterként. | Hubble-törvény: <math>v=Hr</math> ahol H a Hubble-állandó (71 km/s/Mpc). A Hubble-állandó pontos mérése nagyon fontos, mert a Hubble-törvényben szerelő sebességet a vörös eltolódás alapján meg tudják mérni, és így ez alapján lehet egy galaxis távolságát meghatározni. Sokáig viszont nem tudták pontosan megmérni a Hubble-állandót, csak nagyságrendileg tudták meghatározni, ezért azt mondták, hogy <math>H=100h</math> km/s/Mpc, és <math>h</math>-t meghagyták a képletekben paraméterként. | ||
| − | == A HR diagram és a csillagfejlődés szemléletes képe, kompakt objektumok: fehér törpék, neutroncsillagok, fekete lyukak | + | == A HR diagram és a csillagfejlődés szemléletes képe, kompakt objektumok: fehér törpék, neutroncsillagok, fekete lyukak== |
Ahhoz, hogy egy csillag keletkezzen egy gázfelhőből a sűrűségének meg kell haladnia egy kritikus értéket. Ez történhet úgy, hogy egy szupernova robbanás összenyomja a környező gázt vagy a galaxiskarokban, amik haladó sűrűséghullámok vagy pedig galaxisok ütközésekor. A galaxisok ütközésekor nagyon kicsi annak a valószínűsége, hogy a konkrét csillagok ütközzenek, de a galaxisban lévő gázfelhők ütköznek, és ezekben sok új csillag születhet. | Ahhoz, hogy egy csillag keletkezzen egy gázfelhőből a sűrűségének meg kell haladnia egy kritikus értéket. Ez történhet úgy, hogy egy szupernova robbanás összenyomja a környező gázt vagy a galaxiskarokban, amik haladó sűrűséghullámok vagy pedig galaxisok ütközésekor. A galaxisok ütközésekor nagyon kicsi annak a valószínűsége, hogy a konkrét csillagok ütközzenek, de a galaxisban lévő gázfelhők ütköznek, és ezekben sok új csillag születhet. | ||
| 95. sor: | 88. sor: | ||
A csillagok luminozitása és a tömege között kapcsolat van (<math>L</math>~<math>{M^{3,5}}</math>), a csillag élettartamára pedig igaz, hogy | A csillagok luminozitása és a tömege között kapcsolat van (<math>L</math>~<math>{M^{3,5}}</math>), a csillag élettartamára pedig igaz, hogy | ||
| − | <math>t\sim\frac{M}{L}</math> | + | <math>t\sim\frac{M}{L}\sim{M^{-2,5}}</math> |
Tehát minél nagyobb a csillag tömege, annál gyorsabban elfejlődik, élettartama annál rövidebb. | Tehát minél nagyobb a csillag tömege, annál gyorsabban elfejlődik, élettartama annál rövidebb. | ||
| − | + | ==A csillagok energiatermelése:== | |
p-p lánc: | p-p lánc: | ||
| 143. sor: | 136. sor: | ||
Vöröseltolódás: ld. Doppler-effektus. Akkor lép fel, ha egy objektum távolodik tőlünk, színe egyre vörösebb lesz, a színképvonalai a hosszabb hullámhosszak felé tolódnak el. A világegyetem tágulása miatt a kozmikus objektumnál ez a jelenség lép fel, és a Hubble-törvénynek megfelelően minél távolabb van egy objektum, annál nagyobb a vöröseltolódása. Ezen a jelenségen épp ezért távolságmeghatározási módszerek is alapulnak. A vöröseltolódás ellentettje a kékeltolódás, amikor egy égitest közeledik felénk (pl. Androméda-galaxis, a Tejútrendszer spirálgalaxis szomszédja). | Vöröseltolódás: ld. Doppler-effektus. Akkor lép fel, ha egy objektum távolodik tőlünk, színe egyre vörösebb lesz, a színképvonalai a hosszabb hullámhosszak felé tolódnak el. A világegyetem tágulása miatt a kozmikus objektumnál ez a jelenség lép fel, és a Hubble-törvénynek megfelelően minél távolabb van egy objektum, annál nagyobb a vöröseltolódása. Ezen a jelenségen épp ezért távolságmeghatározási módszerek is alapulnak. A vöröseltolódás ellentettje a kékeltolódás, amikor egy égitest közeledik felénk (pl. Androméda-galaxis, a Tejútrendszer spirálgalaxis szomszédja). | ||
| + | |||
| + | Definíció: <math>z=\frac{\Delta\lambda}{\lambda}</math> | ||
| + | |||
| + | <span style="color: red">'''Rudi megjegyzése''':</span> a vöröseltolódásban nem csak a Doppler-effektus játszik szerepet. Nagy távolságokon a skálafaktor növekedése "megnyújtja" az utazó foton hullámhosszát, ezért lesz a fény vörösebb, mint kiindulásának pillanatában. Mivel a hosszú utat megtett fotonok kibocsájtásának pillanatában (vagyis nagyon régen) a forrás hozzánk viszonyított sebessége még kisebb volt, nem is lehetne teljesen a Doppler-effektussal magyarázni a dolgot. Az egész csak árnyalatnyi dolog, főleg mert az így kapott vöröseltolódás pont akkora, mintha az éppen most kibocsájtott foton vöröseltolódását számolnánk tisztán Doppler-effektussal, vagyis ha csak Dopplernek tekintjük, akkor is ugyanazokat az eredményeket kapjuk. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
{{Záróvizsga}} | {{Záróvizsga}} | ||
A lap jelenlegi, 2011. június 27., 19:56-kori változata
Tartalomjegyzék
- 1 Newton-féle gravitációs erőtörvény
- 2 Az ősrobbanás elmélet alapvető feltevései
- 3 Friedmann-egyenletek szemléletes értelme
- 4 Galaxisok kialakulása, morfológiája, Hubble törvény
- 5 A HR diagram és a csillagfejlődés szemléletes képe, kompakt objektumok: fehér törpék, neutroncsillagok, fekete lyukak
- 6 A csillagok energiatermelése:
- 7 Megfigyelés alapjai: luminozitás, magnitúdó, vöröseltolódás
Newton-féle gravitációs erőtörvény
A gravitáció négy alapvető kölcsönhatás egyike az univerzumban, és az egyetlen amely a nagyskálás szerkezetet meghatározza. A legkorábbi kvantitatív megfogalamzása Newton-hoz köthető:
azaz az elektrosztatikus Coulomb-törvényhez hasonló alakú, reciproknégyzetes lecsengésű erő, amely azonban csak vonzó formában ismert. A Newton-i erőtörvény igen jó leírását adta a gravitációs jelenségeknek, a kevés hiányosságot Einstein általános relativitáselmelete pótolta. Ez utóbbi határeseteként tartalmazza a Newton-i erőtörvényt.
Az ősrobbanás elmélet alapvető feltevései
A Big Bang modell a kozmológia Standard modellje. Elsősorban megfigyelésekre és az általános relativitáselméletre épül.
- Az univerzum megfigyelések szerint nagy skálán (100 MPc felett) homogén (az anyag eloszlása egyenletes), erre alapul a kozmológiai elv, vagyis az a feltételezés, hogy univerzum homogén és izotrop.
- Megfigyelések szerint az univerzum tágul (a Hubble-törvénynek megfelelően), ha ezt a folyamatot időben megfordítjuk, akkor eljutunk az ősrobbanás alap gondolatához.
Az ősrobbanás modelljének legfontosabb bizonyítékai:
- Hubble-törvény
- Könnyű elemek előfordulási gyakorisága (75% H és 25% He)
- Kozmikus háttérsugárzás
Friedmann-egyenletek szemléletes értelme
Az univerzum tágulásának tárgyalásakor elengedhetetlen az általános relativitás elmélet kereteiben történő tárgyalás. Tömören összefoglalva a tér-idő távolságokat magábanfoglaló ívelemnégyzet (lásd itt) függ a helytől, és ez a függés kapcsolatban van a tömegekkel. A helyfüggést leíró görbületi tenzor, és az anyag állapotegyenletét magábanfoglaló feszültségtenzor között az Einstein-egyenletek teremtenek kapcsolatot. Ha az univerzum homogén és izotróp, akkor a Robertson-Walker metrika használható, ahol a tágulást egy skálafaktorral (a) jellemezzük az ívelemben:
itt 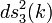 a háromdimenziós ívelemnégyzet függ a térkoordinátáktól, ami különböző geometriájú unierzumoknak felel meg, ezeket k paraméterezi. A fenti ívelemmel az univerzum tágulását leíró Friedmann-egyenletek homogén, izotrop közelítésben:
a háromdimenziós ívelemnégyzet függ a térkoordinátáktól, ami különböző geometriájú unierzumoknak felel meg, ezeket k paraméterezi. A fenti ívelemmel az univerzum tágulását leíró Friedmann-egyenletek homogén, izotrop közelítésben:
Ezek a kozmológia alapegyenletei.
H a Hubble-paraméter, amely az univerzum tágulását jellemzi és aminek a mai értéke a Hubble-konstans, G a gravitációs konstans, 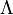 a kozmológiai konstans, c a fénysebesség, k az univerzum görbületét jellemző mennyiség (sík, gömb, vagy hiperbolikus felület). A kozmológiai állandó olyan, hogy pozitív energiasűrűséghez negatív nyomást rendel. Ezzel magyarázzák ma a gyorsuló tágulást, és ezt tartalmazzák a Friedmann egyeletek legjobboldalibb tagjai. Ezért felelős az úgynevezett sötét energia, amiről ma még nem tudjuk, hogy mi is valójában.
a kozmológiai konstans, c a fénysebesség, k az univerzum görbületét jellemző mennyiség (sík, gömb, vagy hiperbolikus felület). A kozmológiai állandó olyan, hogy pozitív energiasűrűséghez negatív nyomást rendel. Ezzel magyarázzák ma a gyorsuló tágulást, és ezt tartalmazzák a Friedmann egyeletek legjobboldalibb tagjai. Ezért felelős az úgynevezett sötét energia, amiről ma még nem tudjuk, hogy mi is valójában.
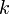 a téridő általános geometriáját adja meg:
a téridő általános geometriáját adja meg:
- A
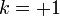 megfelel a pozítív görbületű, zárt térnek, mely határtalan, de véges. Az ilyen geometriájú táguló Univerzum két dimenzióban felfúvódó léggömbbel szemléltethető. Az ilyen térben a háromszög szögeinek összege több, mint 180 fok.
megfelel a pozítív görbületű, zárt térnek, mely határtalan, de véges. Az ilyen geometriájú táguló Univerzum két dimenzióban felfúvódó léggömbbel szemléltethető. Az ilyen térben a háromszög szögeinek összege több, mint 180 fok.
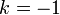 esetben negatív görbületű, nyílt, végtelen térről beszélünk, melynek kétdimenziós megfelelője a nyeregfelület. Ilyen térben a háromszög szögeinek összege kisebb, mint 180 fok.
esetben negatív görbületű, nyílt, végtelen térről beszélünk, melynek kétdimenziós megfelelője a nyeregfelület. Ilyen térben a háromszög szögeinek összege kisebb, mint 180 fok.
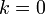 -nál sík, euklidészi térről van szó.
-nál sík, euklidészi térről van szó.
Az egyenletet átalakítva relativisztikus és nem relativisztikus esetekben a következő arányosságokat kaphatjuk:
a, Relativisztikus esetben (sugárzás dominálta univerzum) felhasználva, hogy a nyomás és a sűrűség között a 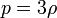 összefüggés áll fenn:
összefüggés áll fenn:
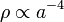 és
és 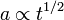
b, Nem relativisztikus esetben (anyag dominálta univerzum) esetén pedig 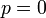 összefüggés teljesülése mellett:
összefüggés teljesülése mellett:
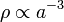 és
és 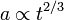
Definiálhatjuk az 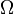 sűrűség paramétert. Ez szemléletesen az univerzum időfejlődését paraméterezi, ha 1-nél kisebb az univerzum örökké tágul, ha 1-el egyenlő akkor a végtelenségig lassul a tágulás, ha nagyobb, akkor egy időután újra összeroppan.
sűrűség paramétert. Ez szemléletesen az univerzum időfejlődését paraméterezi, ha 1-nél kisebb az univerzum örökké tágul, ha 1-el egyenlő akkor a végtelenségig lassul a tágulás, ha nagyobb, akkor egy időután újra összeroppan.
ahol 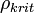 értékét úgy kaphatjuk meg, hogy az első Friedmann egyenletben vesszük a
értékét úgy kaphatjuk meg, hogy az első Friedmann egyenletben vesszük a 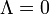 és
és 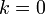 esetet. Ma úgy gondoljuk, hogy
esetet. Ma úgy gondoljuk, hogy 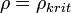 , tehát
, tehát 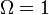 , amit fel lehet írni az univerzum különböző összetevőinek az összegeként:
, amit fel lehet írni az univerzum különböző összetevőinek az összegeként:
ahol ma 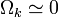 ,
, 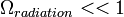 ,
, 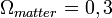 és
és 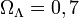 . Itt az
. Itt az 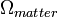 -be tartozik mind a látható, mind a sötét anyag (
-be tartozik mind a látható, mind a sötét anyag (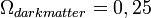 ).
).
Galaxisok kialakulása, morfológiája, Hubble törvény
A galaxisok főleg hidrogénből és héliumból keletkeztek a saját gravitációjuk hatására. Két elmélet létezik:
- Felülről lefelé elmélet: A csillagközi H-ből és He-ból nagy a mai galaxisok méretével összemérhető felhők alakultak ki a saját gravitációjuk miatt, majd ezekben születtek meg a csillagok, amikortól már galaxisnak tekinthetők ezek a képződmények.
- Alulról felfelé elmélet: A csillagközi H és He kis méretű felhőkké állt össze, ezekben születtek az első csillagok. Majd ezek a kis méretű galaxisok ütköztek, és így álltak össze nagy galaxisokká.
A galaxisok osztályozását a Hubble diagram szemlélteti:
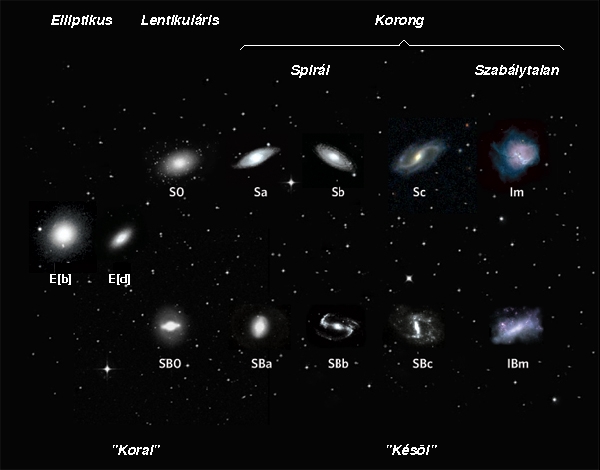
A villa nyelén vannak az elliptikus galaxisok E0-tól E7-ig. Itt a számot az ellipszis tengelyeinek hosszából számolják a 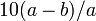 képlettel. Ez természetesen függ attól, hogy a galaxist milyen irányból látjuk. A fölső és az alsó ágon vannak a spirálgalaxisok. Az alsón az úgy nevezett küllős spirál galaxisok (spiral with bar, innen jön az SB rövidítés), ezeknél a spirál karnak van egy egyenes szakasza a maghoz közel. Az S0 az átmenet az elliptikus és a spirál galaxis között, ezt szokták lencse alakúnak vagy lentikulásrisnak nevezni. A mag/korong arány csökken az Sa-tól az Sc-ig, a karok nyílásszöge és a kontrasztossága pedig nő az Sa-tól az Sc-ig. A Hubble-féle osztályozásba a galaxisok 95%-át be lehet sorolni, a maradék 5% az irreguláris galaxisok. Ilyenek például az ütköző galaxisok, érdekesség, hogy a nagyon messzi galaxisoknak az 50%-a irreguláris.
képlettel. Ez természetesen függ attól, hogy a galaxist milyen irányból látjuk. A fölső és az alsó ágon vannak a spirálgalaxisok. Az alsón az úgy nevezett küllős spirál galaxisok (spiral with bar, innen jön az SB rövidítés), ezeknél a spirál karnak van egy egyenes szakasza a maghoz közel. Az S0 az átmenet az elliptikus és a spirál galaxis között, ezt szokták lencse alakúnak vagy lentikulásrisnak nevezni. A mag/korong arány csökken az Sa-tól az Sc-ig, a karok nyílásszöge és a kontrasztossága pedig nő az Sa-tól az Sc-ig. A Hubble-féle osztályozásba a galaxisok 95%-át be lehet sorolni, a maradék 5% az irreguláris galaxisok. Ilyenek például az ütköző galaxisok, érdekesség, hogy a nagyon messzi galaxisoknak az 50%-a irreguláris.
Hubble-törvény: 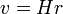 ahol H a Hubble-állandó (71 km/s/Mpc). A Hubble-állandó pontos mérése nagyon fontos, mert a Hubble-törvényben szerelő sebességet a vörös eltolódás alapján meg tudják mérni, és így ez alapján lehet egy galaxis távolságát meghatározni. Sokáig viszont nem tudták pontosan megmérni a Hubble-állandót, csak nagyságrendileg tudták meghatározni, ezért azt mondták, hogy
ahol H a Hubble-állandó (71 km/s/Mpc). A Hubble-állandó pontos mérése nagyon fontos, mert a Hubble-törvényben szerelő sebességet a vörös eltolódás alapján meg tudják mérni, és így ez alapján lehet egy galaxis távolságát meghatározni. Sokáig viszont nem tudták pontosan megmérni a Hubble-állandót, csak nagyságrendileg tudták meghatározni, ezért azt mondták, hogy 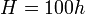 km/s/Mpc, és
km/s/Mpc, és 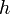 -t meghagyták a képletekben paraméterként.
-t meghagyták a képletekben paraméterként.
A HR diagram és a csillagfejlődés szemléletes képe, kompakt objektumok: fehér törpék, neutroncsillagok, fekete lyukak
Ahhoz, hogy egy csillag keletkezzen egy gázfelhőből a sűrűségének meg kell haladnia egy kritikus értéket. Ez történhet úgy, hogy egy szupernova robbanás összenyomja a környező gázt vagy a galaxiskarokban, amik haladó sűrűséghullámok vagy pedig galaxisok ütközésekor. A galaxisok ütközésekor nagyon kicsi annak a valószínűsége, hogy a konkrét csillagok ütközzenek, de a galaxisban lévő gázfelhők ütköznek, és ezekben sok új csillag születhet.
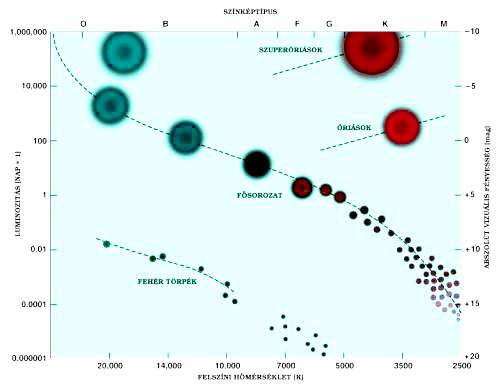
A Hertzsprung-Russel Diagram (HRD) a csillagok hőmérsékletét és a hozzátartozó fényességet szemlélteti. A diagramon kirajzolódó ágak azokat a csillagfejlődési állapotokat mutatják, ahol a csillagok huzamosabb időt eltöltenek. A csillagok fejlődésük során változtatják a helyüket a HRD-n, attól függően, hogy kis (<4 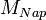 ), vagy nagytömegű (>4
), vagy nagytömegű (>4 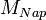 ) csillagokról beszélünk, más-más fejlődési utat járnak be.
) csillagokról beszélünk, más-más fejlődési utat járnak be.
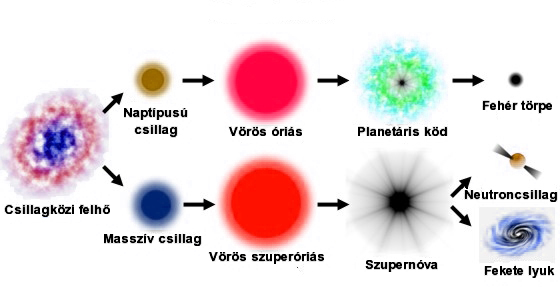
A főágon tartózkodó csillagokban H-fúzióval történik az energiatermelés, amikor viszont a a H elfogyott, nehezebb elemek fúziója kezdődik meg, a csillag vörös-óriássá válik, és átkerül az óriás ágra. Ha a H elfogy egy csillagban, akkor a gravitáció összehúzza, így felmelegszik, és ezért beindul a He fúziója is, majd ha az is elfogy akkor ugyanúgy a gravitáció összehúzza, és beindulnak a magasabb elemek fúziója is egészen a vasig. Egy kis tömegű csillag (<4 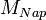 ) esetében a He a legmagasabb, ami tud fuzionálni, amikor ez is elfogy az összehúzódás utáni melegedés miatt keletkező fotonok miatt ledobja légkörét egy planetáris ködöt hagyva maga után, illetve a csillag megmaradt részéből fehér törpe lesz, ami lassacskán kihűl. Amennyiben a csillagnak volt társa, a fehér törpe anyagot szívhat el társcsillagáról, és amikor a tömege eléri a Chandrasekar-határt (1,4 naptömeg), akkor Ia típusú szupernóvarobbánsban felrobban.
) esetében a He a legmagasabb, ami tud fuzionálni, amikor ez is elfogy az összehúzódás utáni melegedés miatt keletkező fotonok miatt ledobja légkörét egy planetáris ködöt hagyva maga után, illetve a csillag megmaradt részéből fehér törpe lesz, ami lassacskán kihűl. Amennyiben a csillagnak volt társa, a fehér törpe anyagot szívhat el társcsillagáról, és amikor a tömege eléri a Chandrasekar-határt (1,4 naptömeg), akkor Ia típusú szupernóvarobbánsban felrobban.
Ha nagytömegű (>4 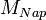 ) csillag elfejlődik, akkor vörös szuperóriás lesz belőle. A csillag magjában az egyre nehezebb elemek fúziója kezdődik meg, egészen a vasig (ez van a potenciálgödör mélyén, eddig mehet a fúzió). A fúzió leállása miatt a hidrosztatikai egyensúly felborul, neutrínók visszapattannak a vasmagról, lökéshullám keletkezik, és II. típusú szupernóva robbanás következik be. A maradvány csillag lehet egy neutroncsillag, vagy fekete lyuk, tömegtől függően (>60
) csillag elfejlődik, akkor vörös szuperóriás lesz belőle. A csillag magjában az egyre nehezebb elemek fúziója kezdődik meg, egészen a vasig (ez van a potenciálgödör mélyén, eddig mehet a fúzió). A fúzió leállása miatt a hidrosztatikai egyensúly felborul, neutrínók visszapattannak a vasmagról, lökéshullám keletkezik, és II. típusú szupernóva robbanás következik be. A maradvány csillag lehet egy neutroncsillag, vagy fekete lyuk, tömegtől függően (>60 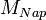 tömegű csillagokból lesz fekete-lyuk, ezalatt pedig neutroncsillag). A neutroncsillagok egy gyorsan forgó változata a pulzár, ahol nem esik egybe a forgástengely és a mágneses tengely. A fehér törpéket és a neutroncsillagokat a degenerált Fermi-gáz nyomása stabilizálja, ez áll ellen a gravitációnak.
tömegű csillagokból lesz fekete-lyuk, ezalatt pedig neutroncsillag). A neutroncsillagok egy gyorsan forgó változata a pulzár, ahol nem esik egybe a forgástengely és a mágneses tengely. A fehér törpéket és a neutroncsillagokat a degenerált Fermi-gáz nyomása stabilizálja, ez áll ellen a gravitációnak.
A HRD vízszintes tengelyén a színképosztályok is szerepelhetnek például, ezeket a hőmérséklet alapján osztották fel. A legfőbb osztályok: O, B, A, F, G, K, M. Ezeken belül 0-tól 9-ig vannak alosztályok is felvéve. A Nap a G2-es osztályba tartozik.
A csillagok luminozitása és a tömege között kapcsolat van (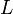 ~
~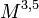 ), a csillag élettartamára pedig igaz, hogy
), a csillag élettartamára pedig igaz, hogy
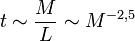
Tehát minél nagyobb a csillag tömege, annál gyorsabban elfejlődik, élettartama annál rövidebb.
A csillagok energiatermelése:
p-p lánc:
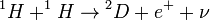
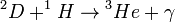
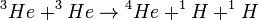
Tehát összességében: 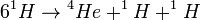 + melléktermékek
+ melléktermékek
Ez jellemző a kisebb csillagokra, pl a Nap magjában is ez a fontos.
CNO ciklus:
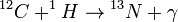
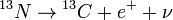
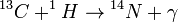
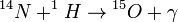
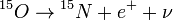
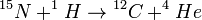
A folyamatban a C, a N, és az O csak katalizátorként vesznek részt. A CNO ciklus a nagyobb csillagokra jellemző.
Megfigyelés alapjai: luminozitás, magnitúdó, vöröseltolódás
Magnitúdó: csillagászati fényességskála egysége: 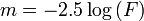 , ahol
, ahol 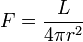 a fluxus és L a luminozitás. Ez utóbbi pedig az égitest által kisugárzott energia minden irányban:
a fluxus és L a luminozitás. Ez utóbbi pedig az égitest által kisugárzott energia minden irányban: 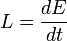 .
.
Két csillag fluxus-arányából a magnitúdó-arányuk:
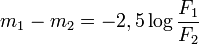
Azért van ott a mínusz jel és a 2,5-ös szorzó faktor, hogy az ókori görögök skálájához hasonlót kapjunk. A magnitúdóskála fordított, tehát minél fényesebb egy csillag, annál kisebb szám a magnitúdója. Létezik relatív (látszólagos) és abszolút magnitúdó. Előbbi a Földről nézve egy objektum fényessége, utóbbi az a fényesség, amit akkor látnánk, ha az objektum 10 pc-re lenne. Az előző képletben  és
és 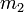 a látszólagos magnitúdók. A Nap látszólagos magnitúdója -27, abszolút magnitúdója pedig +4,83. Egy csillag abszolút fényessége és látszólagos fényessége között a következő összefüggés áll fent:
a látszólagos magnitúdók. A Nap látszólagos magnitúdója -27, abszolút magnitúdója pedig +4,83. Egy csillag abszolút fényessége és látszólagos fényessége között a következő összefüggés áll fent:
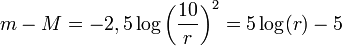
ahol 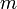 a látszólagos magnitúdó,
a látszólagos magnitúdó, 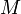 az abszolút magnitúdó és
az abszolút magnitúdó és  a csillag tőlünk mért távolsága pc-ben. Tehát, ha valamilyen módon meghatározhatjuk az objektum abszolút fényességét, akkor a képlet segítségével kiszámolhatjuk a távolságot (a látható fényesség mérhető). Az abszolút fényesség meghatározására több módszer is létezik (periódus-fényesség reláció Cefeidákra és RR Lyr-ekre, SN-k, stb...).
a csillag tőlünk mért távolsága pc-ben. Tehát, ha valamilyen módon meghatározhatjuk az objektum abszolút fényességét, akkor a képlet segítségével kiszámolhatjuk a távolságot (a látható fényesség mérhető). Az abszolút fényesség meghatározására több módszer is létezik (periódus-fényesség reláció Cefeidákra és RR Lyr-ekre, SN-k, stb...).
Vöröseltolódás: ld. Doppler-effektus. Akkor lép fel, ha egy objektum távolodik tőlünk, színe egyre vörösebb lesz, a színképvonalai a hosszabb hullámhosszak felé tolódnak el. A világegyetem tágulása miatt a kozmikus objektumnál ez a jelenség lép fel, és a Hubble-törvénynek megfelelően minél távolabb van egy objektum, annál nagyobb a vöröseltolódása. Ezen a jelenségen épp ezért távolságmeghatározási módszerek is alapulnak. A vöröseltolódás ellentettje a kékeltolódás, amikor egy égitest közeledik felénk (pl. Androméda-galaxis, a Tejútrendszer spirálgalaxis szomszédja).
Definíció: 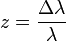
Rudi megjegyzése: a vöröseltolódásban nem csak a Doppler-effektus játszik szerepet. Nagy távolságokon a skálafaktor növekedése "megnyújtja" az utazó foton hullámhosszát, ezért lesz a fény vörösebb, mint kiindulásának pillanatában. Mivel a hosszú utat megtett fotonok kibocsájtásának pillanatában (vagyis nagyon régen) a forrás hozzánk viszonyított sebessége még kisebb volt, nem is lehetne teljesen a Doppler-effektussal magyarázni a dolgot. Az egész csak árnyalatnyi dolog, főleg mert az így kapott vöröseltolódás pont akkora, mintha az éppen most kibocsájtott foton vöröseltolódását számolnánk tisztán Doppler-effektussal, vagyis ha csak Dopplernek tekintjük, akkor is ugyanazokat az eredményeket kapjuk.